途虫数学,分享初中几何精品模型,掌握解决之道。
初中数学有五大常见数学最值模型,分别是将军饮马,费马点,胡不归,阿氏圆和一箭穿心。今天跟大家分享阿氏圆。

什么是阿氏圆
什么是阿氏圆最值模型,说起来话长,我给大家找了一份资料,这也是总结的非常全面的一份资料,大家可以仔细阅读一下,掌握阿氏圆模型的本质和核心解决方案。

初中几何模型阿氏圆
我简单给大家汇总一下,数学模型当中的胡不归和阿氏圆,本质上都是解决AP+kBP的最小值问题。区别在于,胡不归模型的动点在直线上运动,解决的方法是构造正弦三角函数,使Sin乄=K,从而解决K的问题,也就是把kBP转换成另外一条线段,使其系数为1,然后再用三点共线来解决问题。
而阿氏圆的动点p的轨迹是一个圆,它的解决方案是构造子母相似三角形,两个三角形的相似比为k,从而解决k的问题,同样转化成另外一条系数为1的线段。
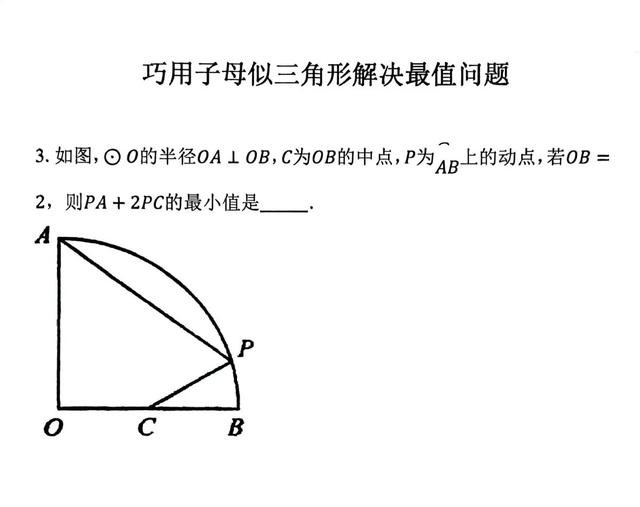
经典习题
这样说显得太抽象,我举三道经典例题来进行说明。上面这道例题,要求PA+2PC的最小值,所以先解决系数2,构造一组子母相似三角形,使其相似比为1:2或者2:1。如下图。

例1参考答案
至于如何构造字母相似三角形?其实并不难,因为子母相三角形都有一个公共角一条公共边,所以先找到这个公共角,然后在其两边分别找出对应线段之比相等,利用两边对应成比例且夹角相等,子母相似三角形就构造出来了。
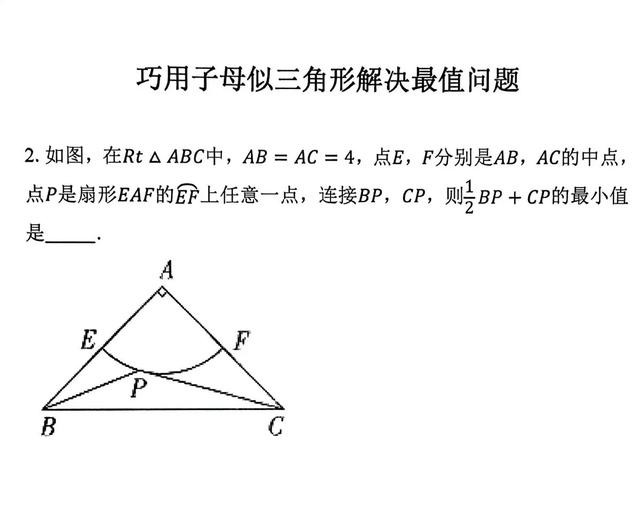
例2
掌握了上面的方法,我们不妨来练习一道题目,这一道题目也是经典的折线拐弯阿氏圆元问题,大家思考一下用哪一个角作为子母相似三角形的公共角?
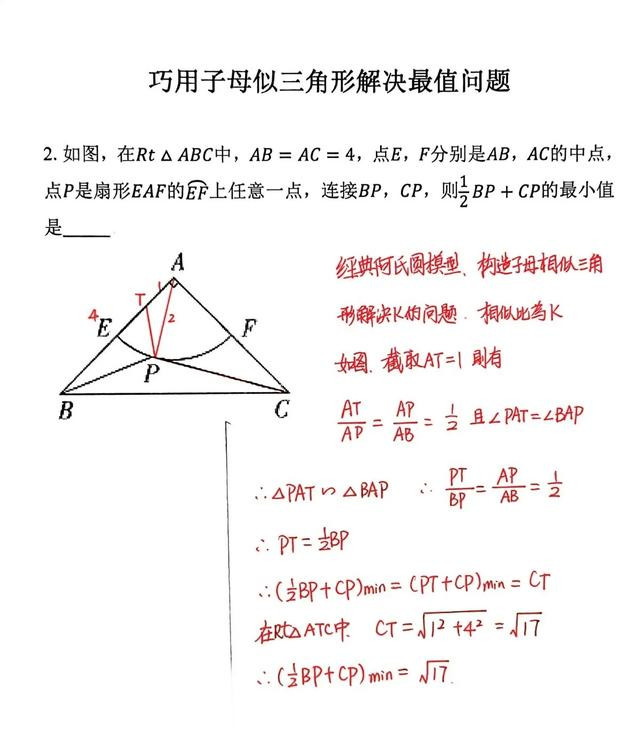
例二参考答案
方法跟例一是差不多的,在数学上,这就是构造和转换的思想,非常重要的数学思想。构造字母相似三角形转换线段,其实,不仅仅利用在阿氏圆的模型当中,它也是一种通用方法。
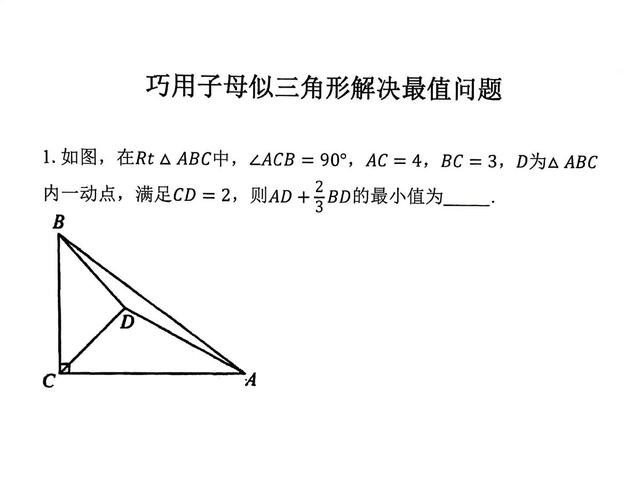
例三
比如上面这道题,粗略一看,它是费马点模型,三线共点通常旋转。但这道题最好用构造子母相似三角形的方法,来解决k的值。具体方法如下。

例三参考答案
这就是阿氏圆模型的主要解决方案,你弄懂了吗?